Algorithm Symbols
A 5x5 Rubik's Cube is also called a Professor's Cube. So if you can solve a 5x5 Rubik's Cube, you are a professor! It must be very difficult. Actually it is not. Similar to a 4x4 cube we solve a 5x5 cube by reducing it down into a 3x3 cube, and there are no special cases. Some people believe that it is even easier than a 4x4.
Fix The Center 3x3 Block
The first step in solving a 5x5 Rubik's Cube is to fix the six 3x3 center blocks.
This step is easier than in a 4x4 cube because the relative positions of the 3x3 center blocks
are determined by the center piece on each side.
We can solve the center block using similar methods as the 4x4 cube.
For each 3x3 center block, we usually start with the center 1x3 block
and then add the two other 1x3 blocks.
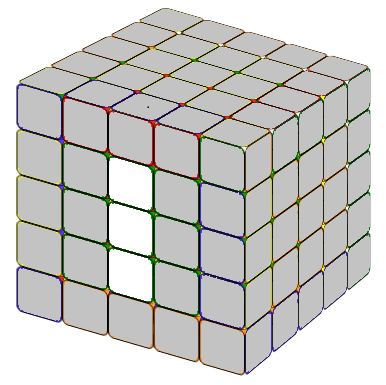
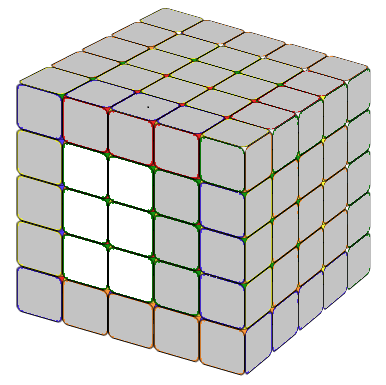
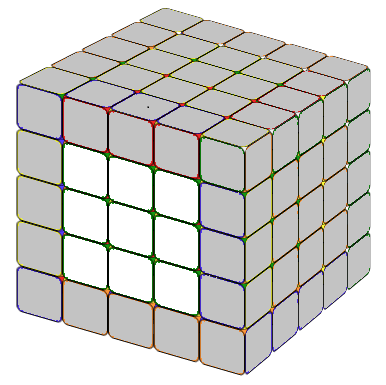
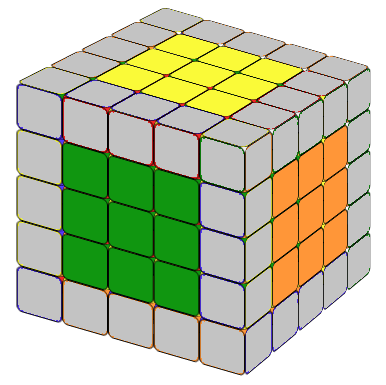
The first few centers are always easier. The last two centers may be a little difficult. The following formulas might help you.
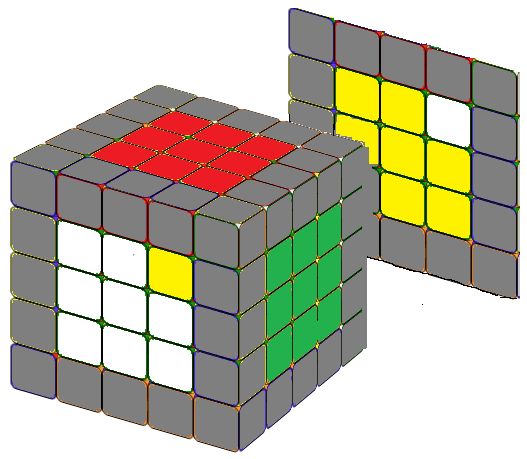
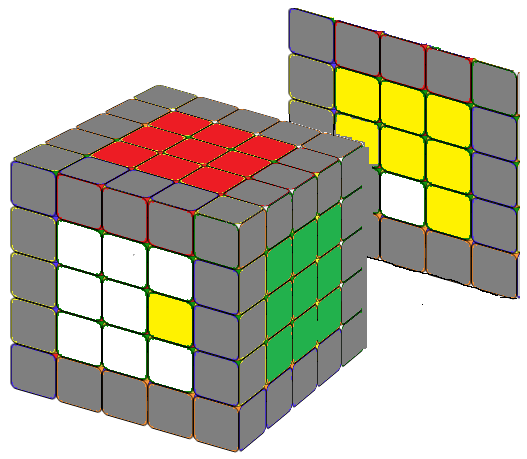
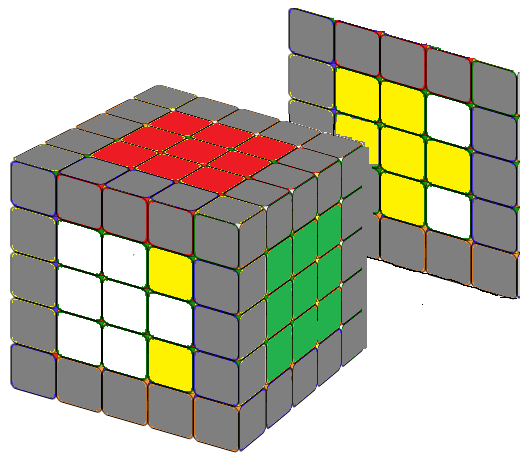
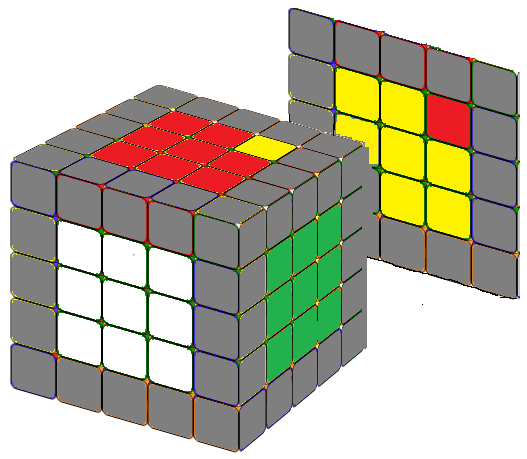
Note that since r2' = r2, you can interchange r2 and r2' in the first three formulas as you wish. We can solve a 5x5 cube center blocks the same way as we solve a 4x4 cube, i.e., we solve it in pairs (white-yellow), (red-orange), (green-blue). If you proceed in this way, you do not need the last formula. We included it just for fun, because it is almost identical to the formula for the counterclockwise fish pattern in a 3x3 cube. Just replace the R or R' with r or r'.
For the first situation, where we need to replace only one piece and this piece is not the center of the 1x3 block, place the cube exactly as shown in the above image, then we can apply the formula r2' B r2 B r2' B2 r2 .
For the second situation, where we need to replace one piece and this piece is the center of the 1x3 blocks of the last two unsolved center blocks, place the two 1x3 blocks exactly as shown in the above image, then simply apply r2' B r2, the cube will now look similar to the first situation.
For the third situation, where the centers of the 1x3 block of the last two unsolved centers are correct, but the other two are wrong, apply the same formula r2' B r2 B r2' B2 r2, the cube will look similar to the first situation.
Combining The Edges.
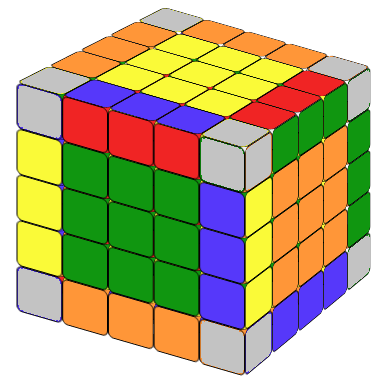Combining edges in a 5x5 Rubik's Cube is time-consuming but intuitive. Similar to solving a 4x4 cube, we rely mostly on formula
Obtain the 1x2 block
The complete formula in this section will also use notation such as 3U, which means that we turn three layers (U and the two layers below it) together in the same direction as U. The concept is the same for 3U' or 3D.A solved 1x3 edge block in a 5x5 Rubik's cube consists of one inner edge (on the third layer) and two outer edges (on the second and fourth layer). Before obtaining a 1x3 edge block, we need to acquire a 1x2 block that includes the inner edge.
To achieve the desired 1x2 block, start by identifying the necessary edge pieces. Then, place the inner edge that we want to combine on the right side. The methods are illustrated below.
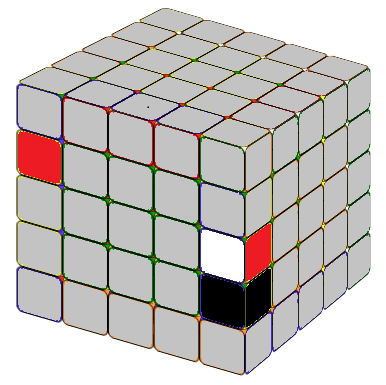
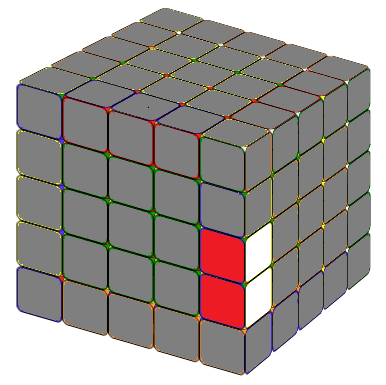
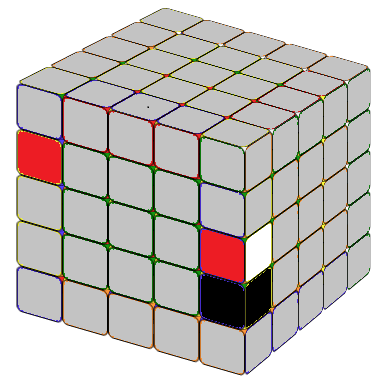
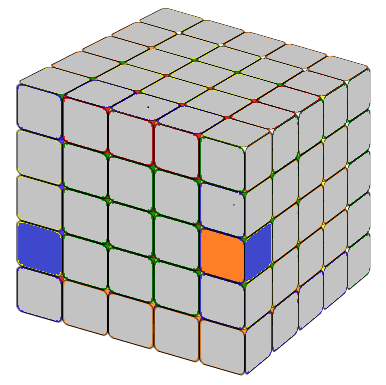
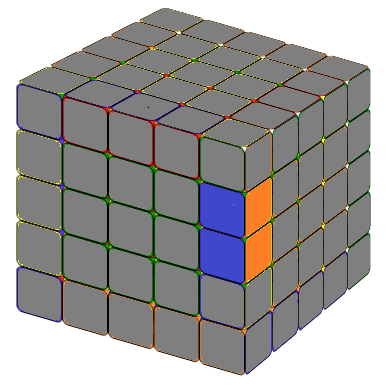
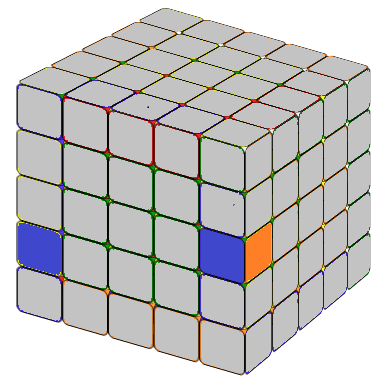
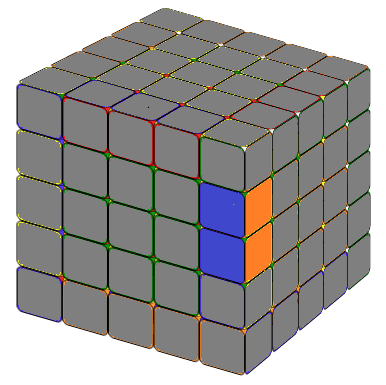
Obtain the 1x3 block
To obtain the 1x3 block, arrange the 1x2 blocks with the inner edge on the right side and place the single edge cubie on the left side. Apply the following formulas accordingly.
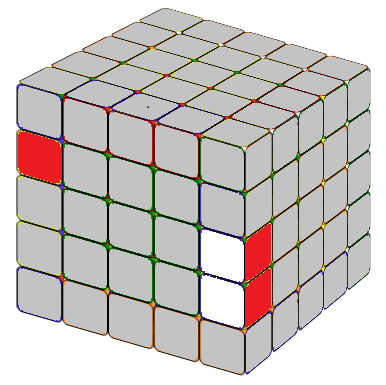
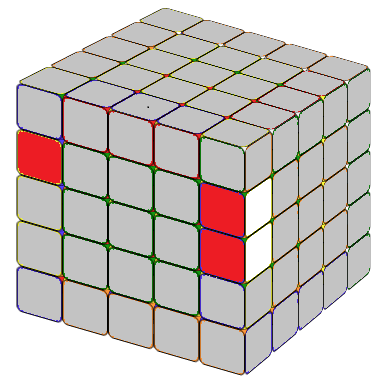
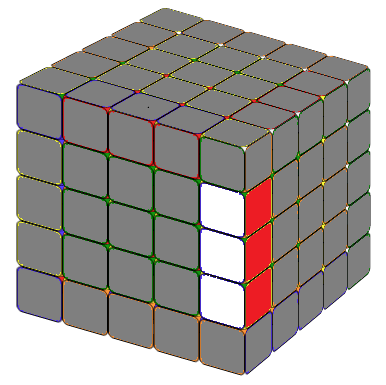
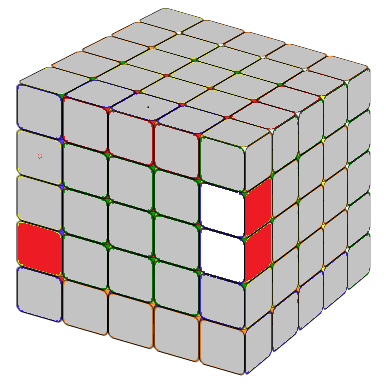
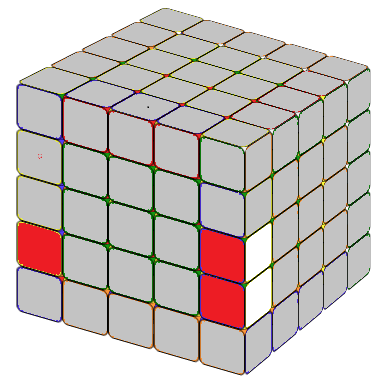
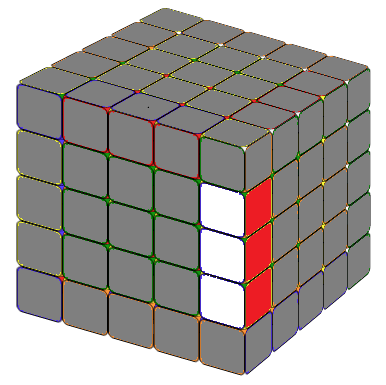
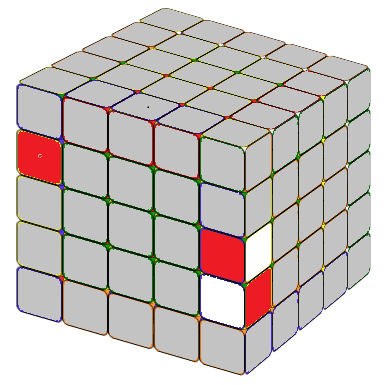
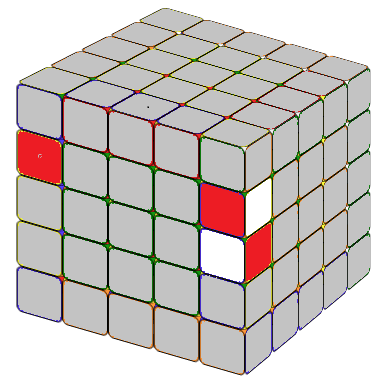
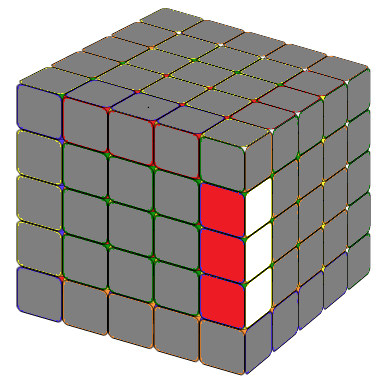
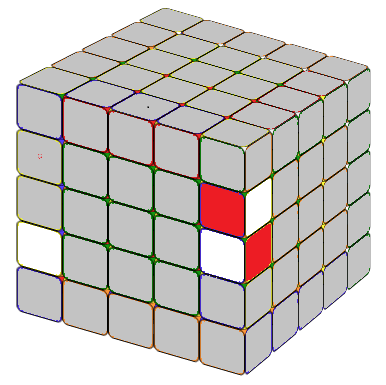
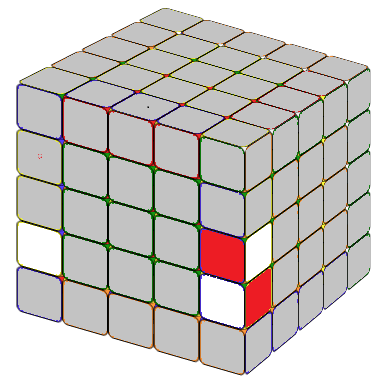
THE LAST UNSOLVED EDGE
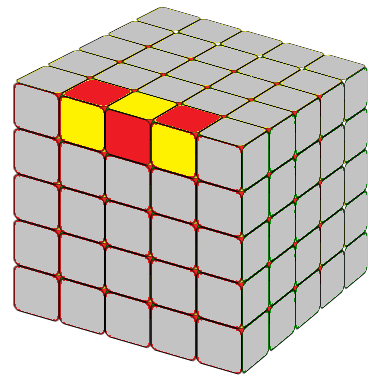
Notice that this is very similar to the 4x4 special case formula except an M after lU2. In the practice Mr'=3R', hence, M(r'U2) means we move three layers on the right hand side together, in direction R', then U2. x means rotate the entire tube 90 degree away from you.
STEP 3: SOLVE THE 5x5 CUBE AS IT IS A 3x3 CUBE
Now we have a 5x5 cube with a 3x3 solved center block and 12 solved 1x3 edge blocks.
We can solve it just like a 3x3 cube.
Congratulations! You have successfully solved the 5x5 Rubik's Cube.
Enjoy your accomplishment!