Algorithm Symbols
Solve The Center 2x2 Blocks.
Let's explore how to solve a 4x4 cube. The most common approach is to reduce the 4x4 cube into a 3x3 cube, for which we already know the solution..

Unlike 3x3 cubes with fixed centers, we need to be mindful of the relative positions of center blocks in a 4x4 cube. Incorrect orientation of the center blocks can prevent cube solving. Orient the cube as follows: yellow on top, white at the bottom, red in front, orange at the back, green on the right, and blue on the left. If you're unsure about the orientation, keep a solved 3x3 cube nearby for reference.
To solve the center block, we typically start with a 1x2 block and then add another 1x2 block without altering the already solved center block. The first four centers are usually straightforward. If you face challenges with the last two center blocks, consider using the following two formulas for assistance.
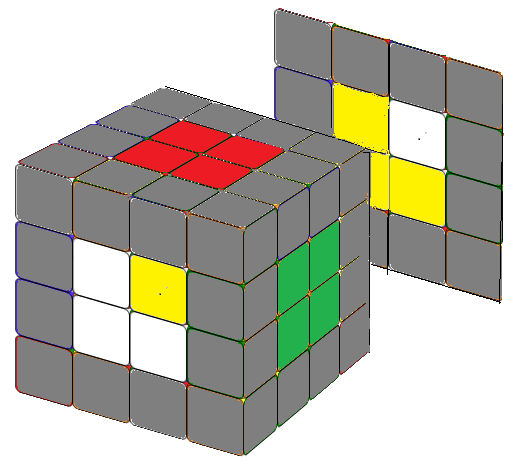
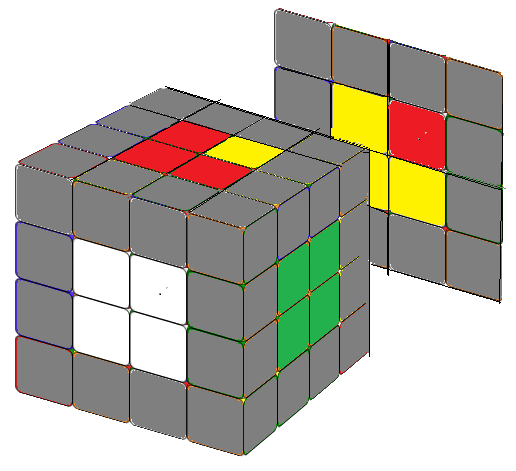
Note that since r2' = r2, you can freely interchange r2 and r2' in the first formulas. When solving a 4x4 cube, it's beneficial to work in pairs such as (white-yellow), (red-orange), and (green-blue). This approach reduces confusion about the relative positions of the center middle blocks. If you solve it in pairs, you won't need the second formula. However, we've included it for enjoyment as it closely resembles the formula for the counterclockwise fish pattern in a 3x3 cube. Simply replace R or R' with r or r'.
Animation: Fix the centerCombining The Edges.
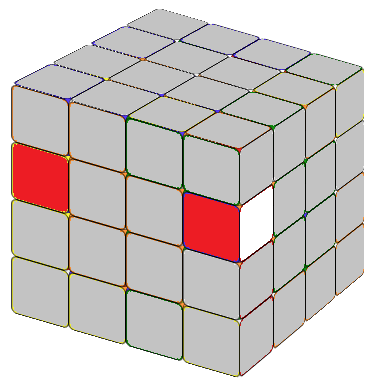
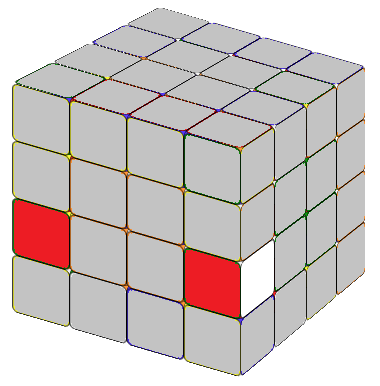
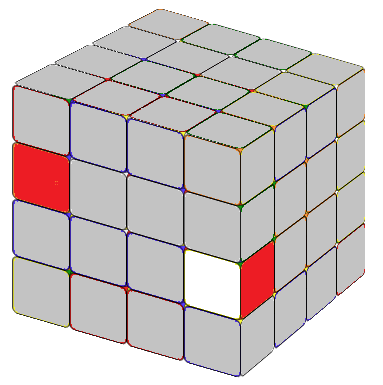
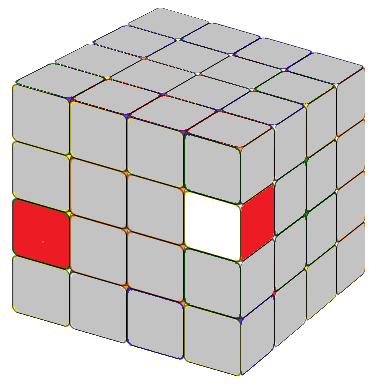
There are multiple approaches to do this, and you can find numerous formulas online. Recently, I learned a method that, in my opinion, is the best one yet. In a 4x4 cube, completed edges consist of two edge cubies. Our first step is to locate the two edge cubies we want to combine. If these edge cubies are on the same layers but different sides (refer to as Fig. 2.1 or Fig. 2.2), we can apply the formula:
Tip: We know that an edge cubie displays two visible sides. The formula R U R' F R' F' R will reverse the colors of these two sides and exchange the position of the edge cubie from the second layer with the edge cubie from the third layer on the right side. The core part of these two formulas is exactly the same, and that's the only formula we need to remember to combine the edges efficiently.
Practice with the formula, you will master it in no time.
SOLVE THE 4x4 CUBE AS IT IS A 3x3 CUBE
Now you can solve your 4x4 Rubik's Cube with solved centers (2x2 blocks) and edges (1x2 blocks) just like a 3x3 cube! However, sometimes, you will encounter situations unique to the 4x4 cube that you won't encounter in a 3x3 cube.
SPECIAL CASES IN 4x4 CUBE
Consider these two special situations:
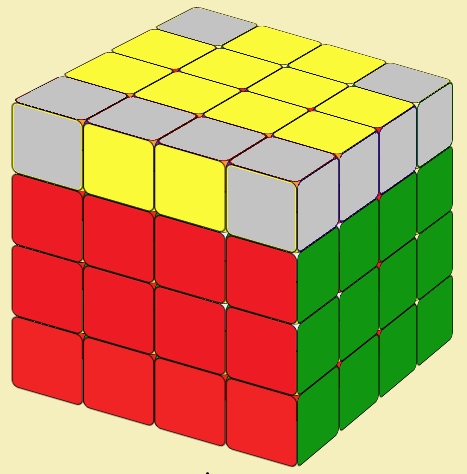 Could not make a yellow cross
Could not make a yellow cross
 Need to exchange two edges
Need to exchange two edges


The following formula will help you if you could not make a yellow cross using only formulas from 3x3 cube.
If in the last step, you need to exchange only two edges, you can use the following simple formula which will bring the cube back to situations that could be solved as a 3x3 cube:
Now you have solved the 4x4 Rubik's Cube. Enjoy!